[最も人気のある！] フィボナッチ数列 階段 331141-フィボナッチ数列 階段 漸化式

May 26, 17 · まずは、フィボナッチ数列とは何かについて説明します。 数列で説明 フィボナッチ数列は、「2つ前の項と1つ前の項を足し合わせていくことでできる数列」のことです。数列は「1,1」から始まり、 1, 1, 2, 3, 5, 8, 13, 21 と続いていきます。 これを漸化式で表すと、この値は (1＋√5)/2 で、これはフィボナッチ数列 nが大きいときの Fn の比と同じです。 階段の昇り方 n段の階段を1段、または、2段とびで昇る昇り方はフィボナッチ数になります。(6) Fib（0）= 1の定義はコンビナトリアル定義として知られており、Fib（0）= 0は古典的定義である。

フィボナッチ数列をわかりやすく解説 一般項の求め方をマスターしよう Studyplus スタディプラス

フィボナッチ数列 階段 漸化式

フィボナッチ数列 階段 漸化式-フィボナッチ 数列 （ フィボナッチすうれつ 、 英 Fibonacci sequence ） (Fn) は、次の 漸化式 で定義される： F0 = 0, F1 = 1,4001番目から5000番目までのフィボナッチ数列 5001番目から6000番目までのフィボナッチ数列 6001番目から7000番目までのフィボナッチ数列 7001番目から8000番目までのフィボナッチ数列 8001番目から9000番目までのフィボナッチ数列 9001番目から番目までのフィボナッチ数列 フィボナッチ数列は自然界でよく出てくる 花びらの枚数，木の枝分かれ，まつぼっくりの

Withe通信 フィボナッチ数列と黄金比と美 Withe 広大生学習支援団体 Note

Fibonacci 再帰 フィボナッチ数列 階段 フィボナッチシーケンスでは、fib(0)は0か1ですか?これはフィボナッチ数列です。 したがって、 答えはフィボナッチ数列の 項目の値です。 その求め方については、 数理論 ＞ フィボナッチ数列 をご覧ください。 （2） 階段上り n 段の階段を2つ以上飛ばさずに上る場合の数を考えましょう。フィボナッチ ffibonacci 数列には、加法定理 addition theorem(加法法則 addition law) が成り立ちます。 $ 1 \le m$ のとき、 $$ F_{n m} = F_m F_{n1} F_{m1} F_n $$ フィボナッチ数列の定義は、だれでも知っている単純なものですが、

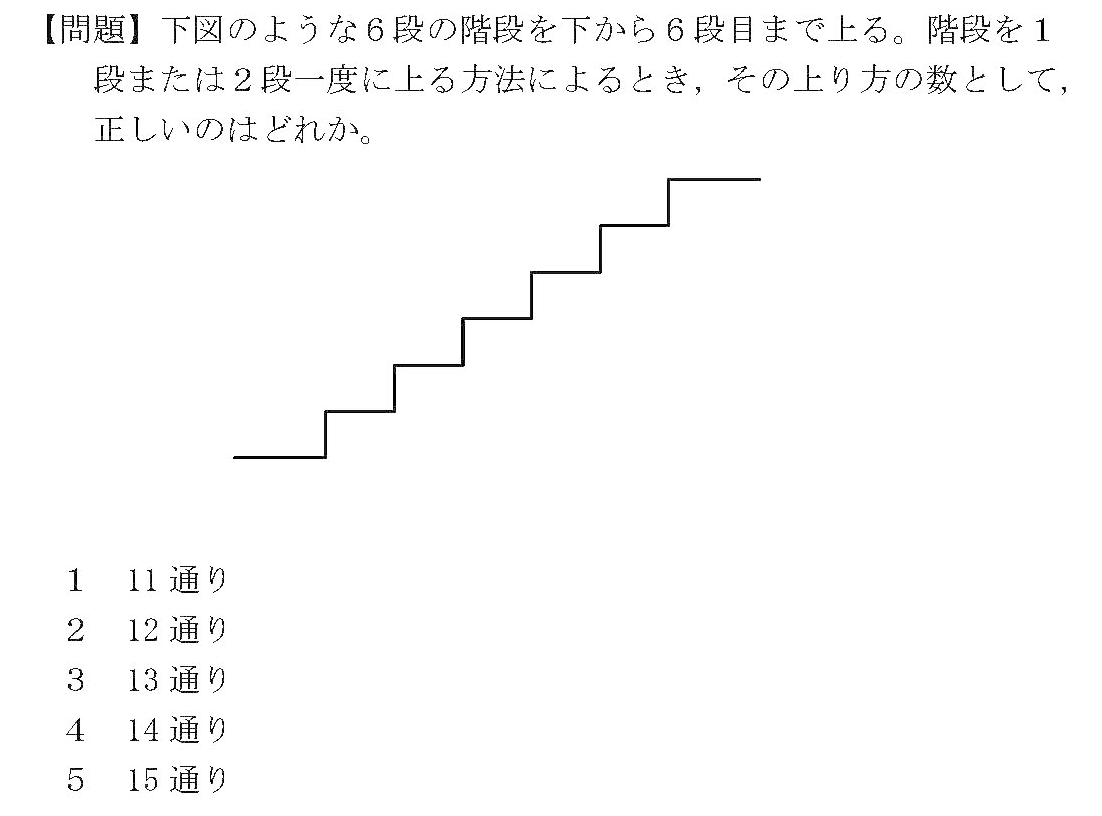
1段または2段づつ移動可能な7段のぼりの場合の数は 「オンボロ階段」などで解説されているように「フィボナッチ数列」で表すことができます。 即ち F n =F n1 F n2 F 0 =1,F 1 =1 より F 7 =21です。階段の上がり方（フィボナッチ数列など） 場合の数で「階段の上がり方」という有名な問題があります。 例えば、次のような感じです。 階段を1歩につき1段か2段で上がるとき、7段の階段の上がり方は何通りありますか。 この問題は決して易しくない（初見だと解けない受験生が多い）のですが、ほとんどの受験生が解法を教わっていることと、解法を知っていれ①フィボナッチ数列 ②リトレースメント という上記の2つの言葉をくっつけています。 ①フィボナッチ数列とは フィボナッチ数列とはイタリアの数学者レオナルド・フィボナッチ氏に因んでつけられた数列のことです。

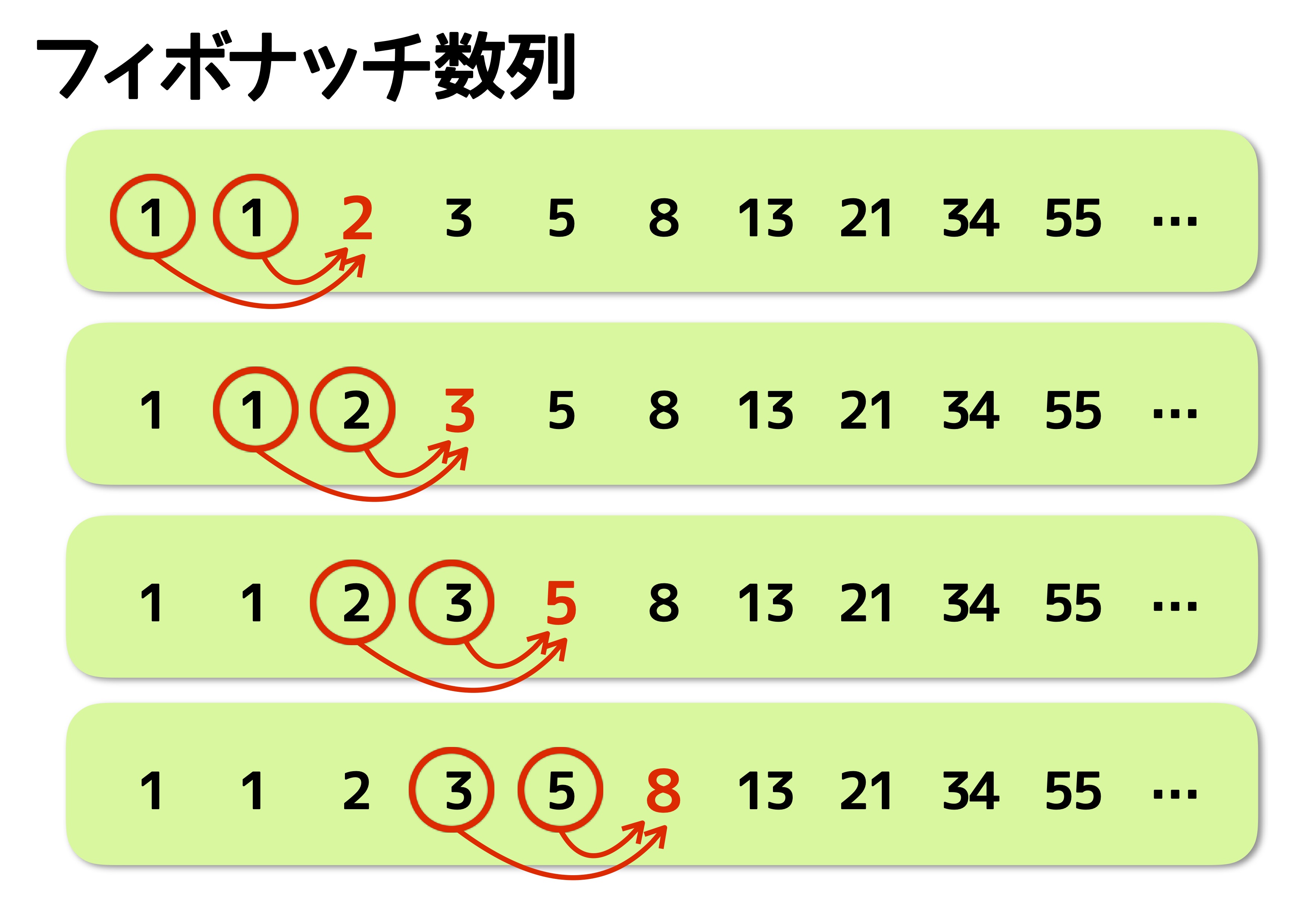
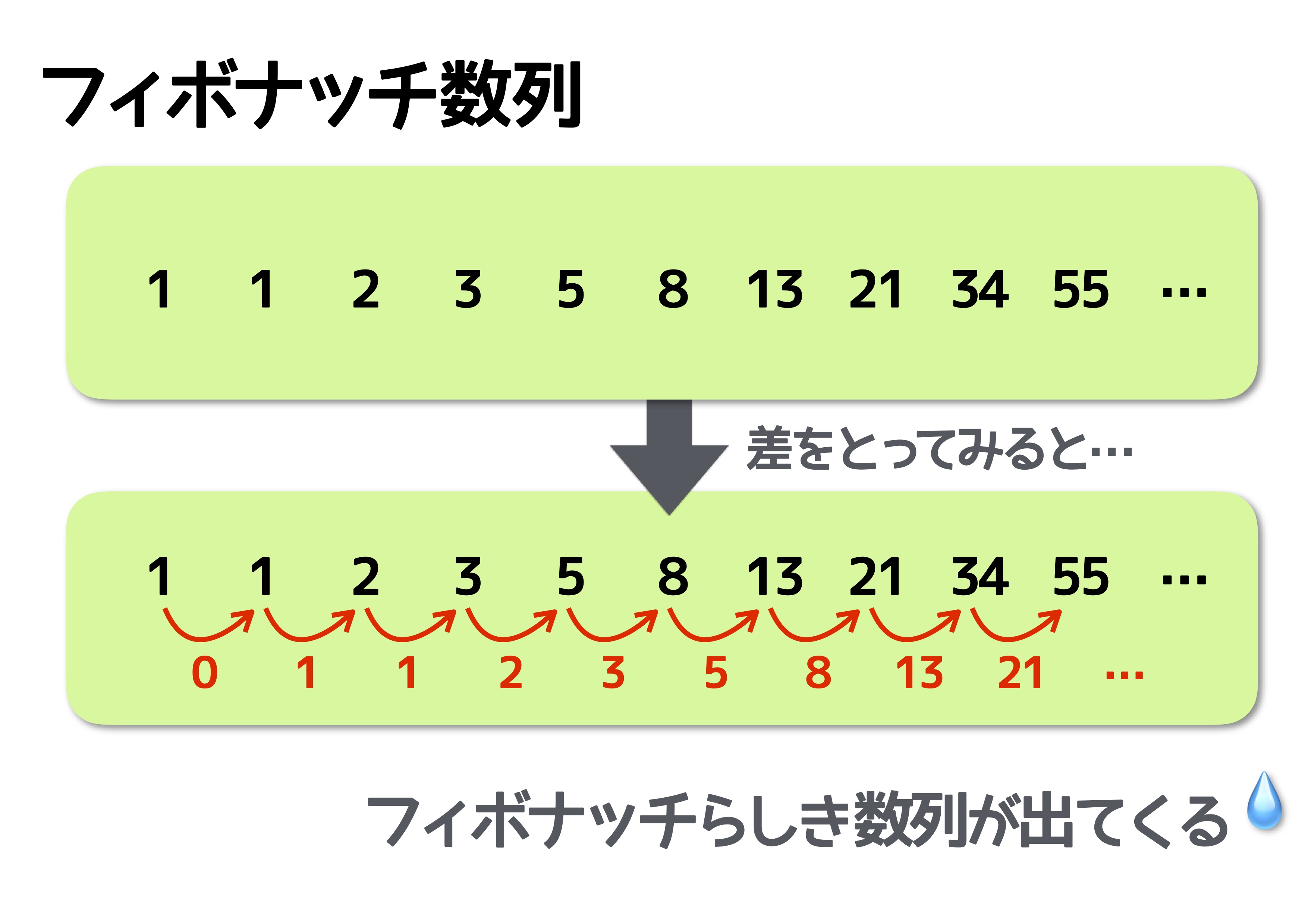
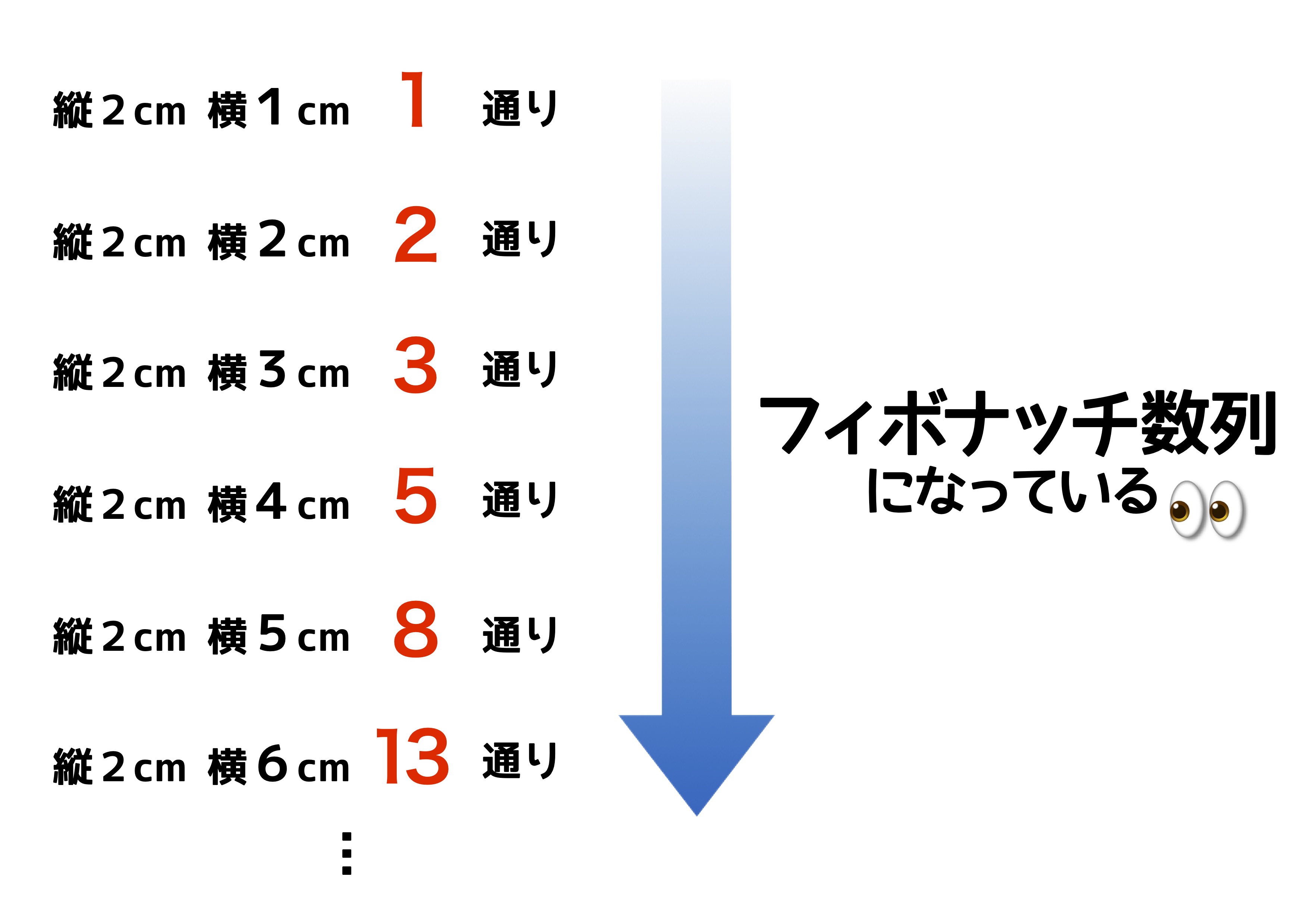
このようにフィボナッチ数列とは、 前の二つの数を足した数が次の数となる という性質を持っています。 黄金比に向かうフィボナッチ数列 フィボナッチ数列を語る上で欠かせないのが、黄金比との関係フィボナッチ数列は、一般に、「前々項前項=自項」となる数列ですので、 (1)前々項と前項 (2)前々項と自項 (3)前項と自項 の三つのうちどれか一つの組み合わせが判れば、三数のうちの残りの数値を求める事がで きます。フィボナッチ数列というのは、 1、1、2、3、5、8、13、21、34、55、 というように、前の2つの数の和が次の数になる数列です。 先ほどの問題のような、「1歩で1段or 2段」で階段を上がる方

問題１１ 06早稲田中 すぐる学習会

フィボナッチの核心 トレンドフォローで絶対に覚えておきたい２つの数字 迷晴れｆｘ

1 1 2 1 3 2 4 3 5 5 6 8 7 13 8 21 9 34 10 55 11 12 144 13 233 14 377 15 610 16 987 17 1597 18 2584 19 4181 6765 21 22 23 24 25 26 27 28 29 30 40 31 32 33 34 35 36 37 381 数列の問題で 階段の登り方の漸化式の立て方が分かりません。 問題はなんでも良いのですが、 まあ、一段 2 フィボナッチ数列です。 数列{fn}の奇数項を抜き出した数列の和を考えます。 f1f3f5Sep 01,  · この数列に関する値は自然界にも出現します。例を挙げると、 ・ヒマワリの種はきれいにできるとフィボナッチ数列の個数でらせん状にできる ・木の枝の本数はフィボナッチ数列に従って増えることが多い

ゆな 動的計画法 道順の書き込み式による求め方 階段登りの場合の数を求める漸化式 書き込み式 フィボナッチ数列と黄金比 場合の数 漸化式 数列 フィボナッチ フィボナッチ数列 黄金比 極限 性質証明

Fibonacci Sequence のアイデア 22 件 フィボナッチ フィボナッチ数列 レオナルド ダ ヴィンチ

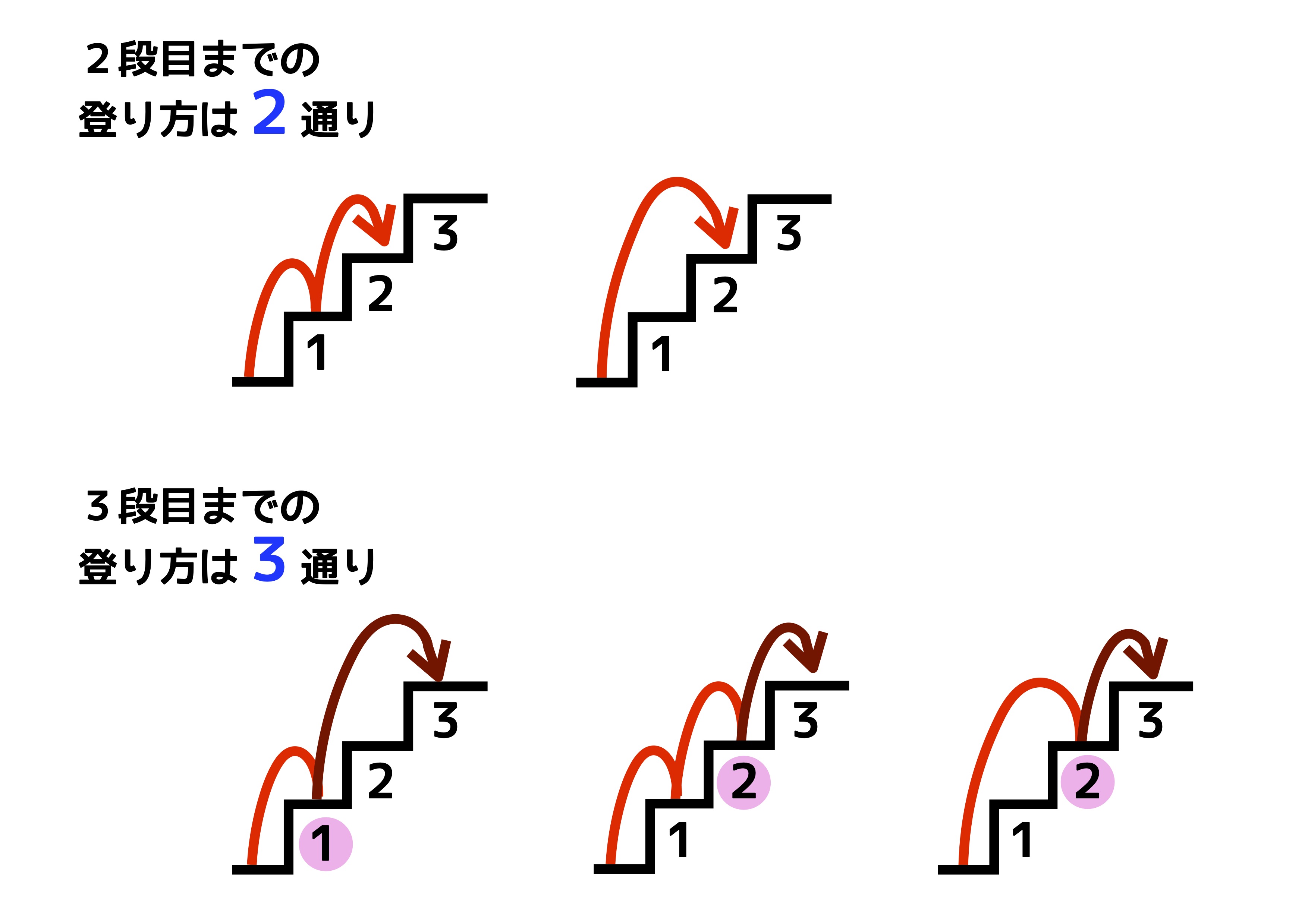
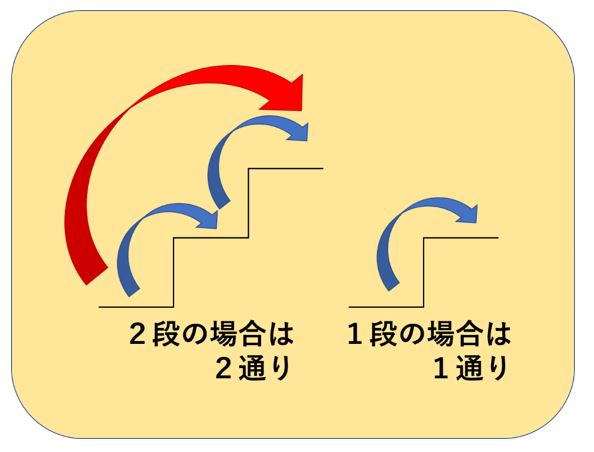
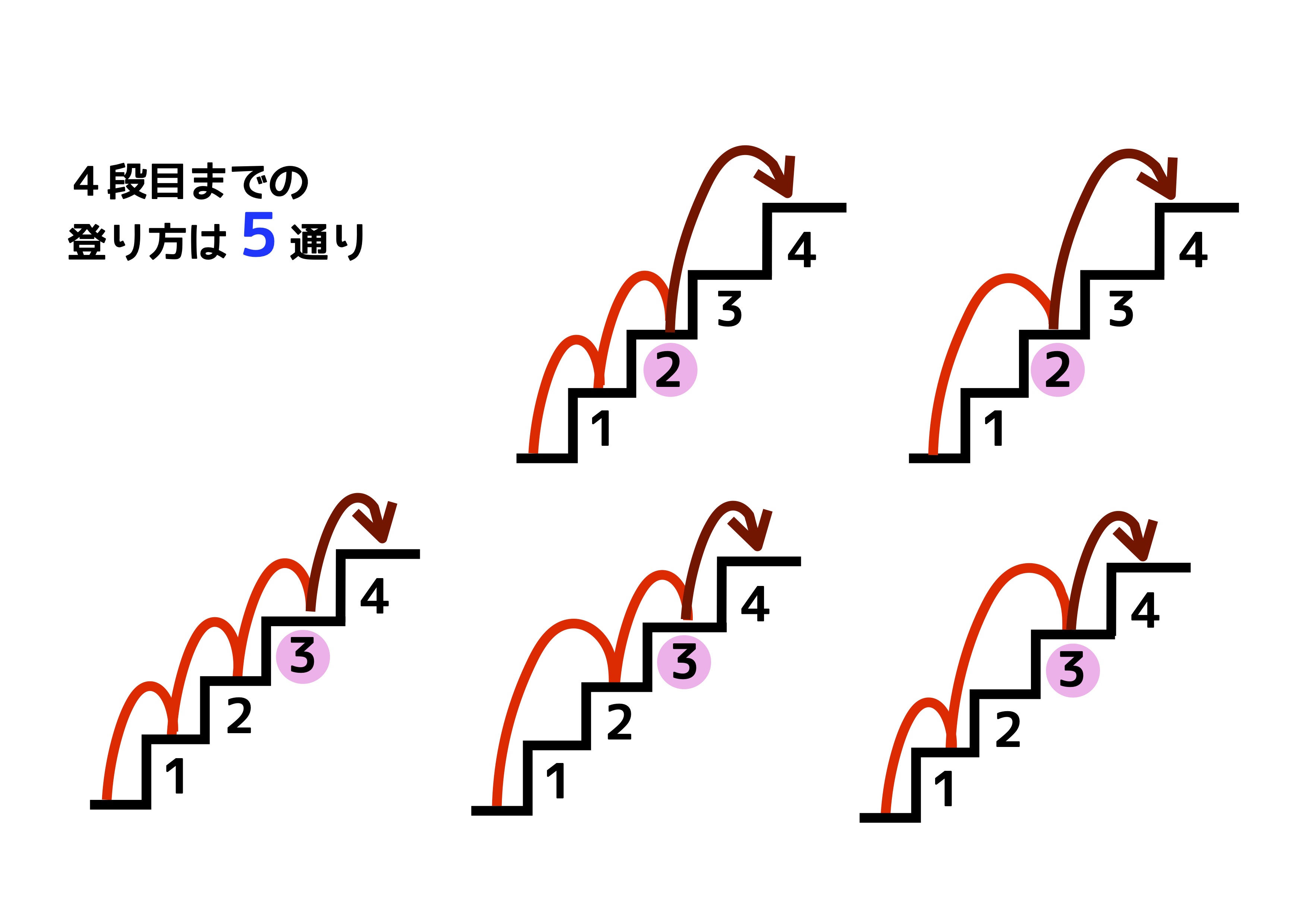
Mar 25,  · つまり、1段2段の上り方のある階段問題は 2つ前か1つ前からしか上がってこれない仕組みとなっている ため、 階段の上がり方はフィボナッチ数列 になります。 まとめ ・階段問題（1,2段）はフィボナッチ ・1つ前、2つ前から来る問題はフィボナッチPerformance 計算 フィボナッチ数列 階段 サブライン時間におけるn番目のフィボナッチ数 (9) サブ線形時間でn番目のフィボナッチ数を計算するアルゴリズムはありますか？ O（log n）算術演算で、サイズO（n）の整数を使用してF（n）を計算する1ライナーが2 2 回答 フィボナッチ数列の質問です。 「N段の階段を1段ずつか2段ずつ（1段とばし）で上るには何通りの上り方があるか」 これはフィボナッチ数列になるとのことですが、腑に落ちません。 （）内の'1段とばし"に意味が フィボナッチ数列の質問です。 「N段の階段を1段ずつか2段ずつ（1段とばし）で上るには何通りの上り方があるか」 これはフィボナッチ

フィボナッチ数列とは 問題に隠れた規則性に気づけるようにしよう 中学受験ナビ

数学b フィボナッチ数列の絵本と階段 学習村の とりあえず国公立へ行こう

フィボナチ数列 13 5 Written by ma{ (caLabo) 1 階段上りの問題 ある人が, 15 段ある階段を上ろうと思います。 上り方は「次の段に上る」か 「1 段飛ばして上る」の2 通りをその都度選べるものとすると, ちょうど15 段 を上り切るまでの登り方は何通りあるか。フィボナッチ数列の中から \(2\) つの数を取り出したとき、その \(2\) 数の最大公約数もフィボナッチ数列の中にある;フィボナッチ数列とは フィボナッチ数列は1,1,2,3,5,8,13,21,34,55となるもので、 11=2 、12=3、 という風に前の数字を足すと次の数字となる数列のこと。 これがfxの世界ではよく効く魔法のコードとしてよく知られている。

フィボナッチ数列の加法定理 理系のための備忘録

中学受験算数 難問 階段の上り方 フィボナッチ数列って知ってる 毎日１題中学受験算数３８ Youtube

フィボナッチ数列 階段 (6) フィボナッチ数は、コンピュータサイエンスの学生のための再帰の一般的な導入となっており、自然の中で存続するという強い主張があります。これらの理由から、私たちの多くはそれらに精通しています。フィボナッチ数列とは 1,1,2,3,5,8,13,21,34,55, という数列は， ・最初の2つが1で ・3つめ以降は「前の2つを足した値」になっています。 例えば， 5 8 = 13 58=13 5 8 = 13 なので， 5, 8, 13 5,8,13 5, 8, 13 が並んでいます。このような数列のことをフィボナッチ数列と言います。(2) あなたは黄金比の魔法を使うことができます：φ=（sqrt（5）1）/ 2とし、 fib（n） =（φn（1φ） n ）/ sqrt（5）を定義します。 そのような関数を明らかな方法で怠惰なリストに変換することができます：Haskellでは以下のように動作し

フィボナッチ数列とは 問題に隠れた規則性に気づけるようにしよう 中学受験ナビ

フィボナッチ数列 9 Youtube

別名「美の数列」とも言われます。 フィボナッチタワーは，スターケージ（星かごパズル）などの考案者，日詰明男さん製作，海猫屋ほかが協賛して商品化されました。 フィボナッチタワー 1100円（本体1000円） （消費税込・送料別）考え方はフィボナッチ数列とまったく同じです。ただし、フィボナッチ数列は最初の2項が「1,1」であるのに対し、階段問題では「1,2」で始まることにご注意ください。 ですから、 🌻n 段の階段を1段または2段ずつ昇るときに、昇る場合の数は Fn1 通りある階段の昇り降り 問題 階段を1歩か2歩で上がるとき、9段の階段の上がり方は ④③より、 これでフィボナッチ数列の一般項が求められました。 フィボナッチ数列の項は全て自然数でありながら、一般項には無理数が現れるという、ちょっと不思議な結果

フィボナッチ数列 英語

中学受験 算数 動画解説 場合の数 階段の上り方 フィボナッチ数列 トリボナッチ数列 Youtube

中学受験 算数 動画解説 場合の数 階段の上り方（フィボナッチ数列・トリボナッチ数列）10 段からなる階段があり，1 段上がりと2 段上がりのN 段の階段を1段または2段ずつ上るときに、上る方法の数を F n1 通りとすると、F n はフィボナッチ数列となる。 これは数学的帰納法で証明できる。 n=1 の時は、1段上りの1通りしかないのでF 2 ＝1で正しい。 n=2 の時は、1段上りと2段上りの2通りがあるので、F 3 ＝2で正しい。

フィボナッチ数列 Hear

算数テク フィボナッチ数列 階段問題 中学受験算数なら開成卒プロ家庭教師k

フィボナッチ数列とは 一般項から 黄金比 と呼ばれる理由まで解説 高校生向け受験応援メディア 受験のミカタ

算数テク フィボナッチ数列 タイル問題 中学受験算数なら開成卒プロ家庭教師k

黄金比 モデュロール フィボナッチ数列 Archicad For Beginners

フィボナッチ数列とは 問題に隠れた規則性に気づけるようにしよう 中学受験ナビ

Memorandum

フィボナッチ数列 京極一樹の数学塾

フィボナッチ数列のスマホ壁紙 検索結果 1 画像数134枚 壁紙 Com

Pichikochan21 On Instagram 赤い誘惑 らせん階段 赤い Aka 美しい 黄金比 フィボナッチ数列 古代ギリシャでは神の比 黄金比1 1 168 パルテノン宮殿 ミロノビーナス 誘惑 Instagram Instagram Posts Table Fan

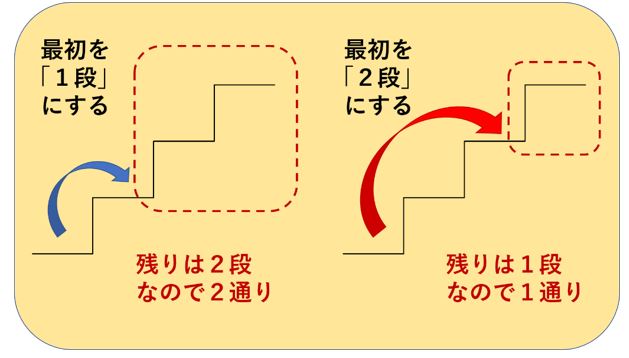
階段上りとフィボナッチ数列と場合分け 中学受験プロ講師ブログ

階段を1段または2段で昇る 07 京都大 理乙 イズミの数学

神の愛した数 フィボナッチ数列 について考えてみよう Ryushoの浪漫紀行

詳細と白のスプレー塗料でスチール製らせん階段のクローズ アップ構造詳細 ねじのストックフォトや画像を多数ご用意 Istock

小６算数 場合の数 階段の登り方 ベネッセのプログラミング教育情報

フィボナッチ数列のbinetの式の導出と理解

フィボナッチ数列 Of 京極一樹の数学塾会員頁

フィボナッチ占い ロマンチック仮想通貨

灘 開成に入る子なら解ける フィボナッチ数列 の問題とは 富裕層向け資産防衛メディア 幻冬舎ゴールドオンライン

フィボナッチ数列 京極一樹の数学塾

北辰塾 情報局 直撃 中学入試問題 第280回 城西川越 規則性 階段状の数表

警視庁16 フィボナッチ数列 岡野朋一 Note

フィボナッチ数列をわかりやすく解説 一般項の求め方をマスターしよう Studyplus スタディプラス

階段上りとフィボナッチ数列と場合分け 中学受験プロ講師ブログ

Toukou

ゆな 動的計画法 道順の書き込み式による求め方 階段登りの場合の数を求める漸化式 書き込み式 フィボナッチ数列と黄金比 場合の数 漸化式 数列 フィボナッチ フィボナッチ数列 黄金比 極限 性質証明

住んでみないと分からないワタマンのメリット デメリット みやままひろ Note

デザインの中に隠された黄金比の秘密を探る Wokobo

算数テク フィボナッチ数列 階段問題 中学受験算数なら開成卒プロ家庭教師k

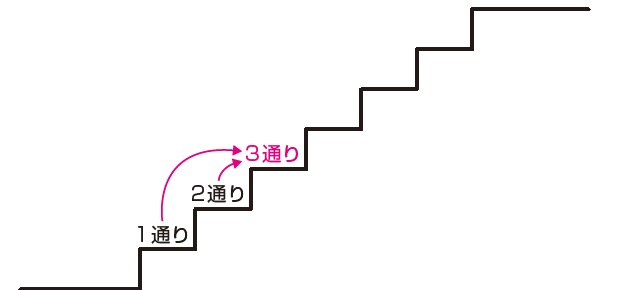
灘 開成に入る子なら解ける フィボナッチ数列 の問題とは 富裕層向け資産防衛メディア 幻冬舎ゴールドオンライン

フィボナッチ数列 数学入試問題

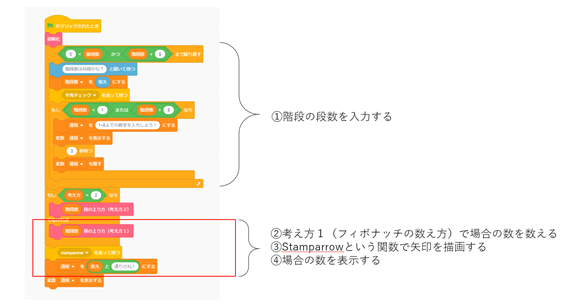
小６算数 場合の数 階段の登り方 ベネッセのプログラミング教育情報

フィボナッチ数 Wikipedia

フィボナッチ数列をわかりやすく解説 一般項の求め方をマスターしよう Studyplus スタディプラス

階段の上り方 フィボナッチの数列 中学受験算数超特急シリーズ 無料版

フィボナッチ数列をわかりやすく解説 一般項の求め方をマスターしよう Studyplus スタディプラス

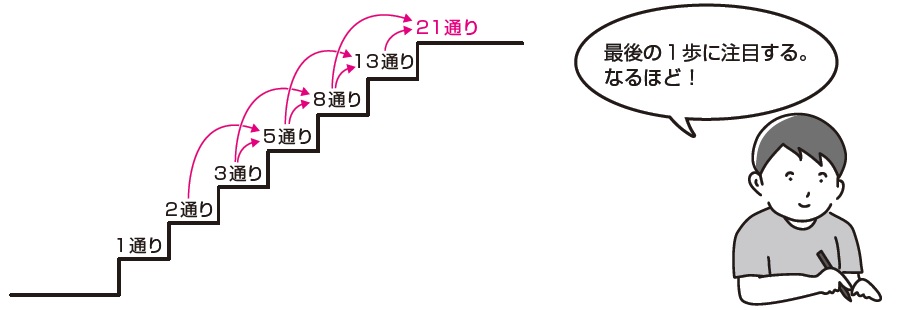
灘 開成に入る子なら解ける フィボナッチ数列 の問題とは 富裕層向け資産防衛メディア 幻冬舎ゴールドオンライン

三乗総和

1 013点のフィボナッチ数列のストックフォト Getty Images

螺旋階段 模型 簡単 Imsmedia Org

すべてはフィボナッチ数列的に進んで行く Lowerleft Works

Collo26

フィボナッチ数列とは 問題に隠れた規則性に気づけるようにしよう 中学受験ナビ

階段の上り方 フィボナッチの数列 中学受験算数超特急シリーズ 無料版

灘 開成の入試に頻出 図形に潜む フィボナッチ数列 の問題 幻冬舎ゴールドオンライン Yahoo ニュース

旅に出たい日常

フィボナッチ数列の加法定理 Qiita

フィボナッチ占い ロマンチック仮想通貨

フィボナッチ数列 京極一樹の数学塾

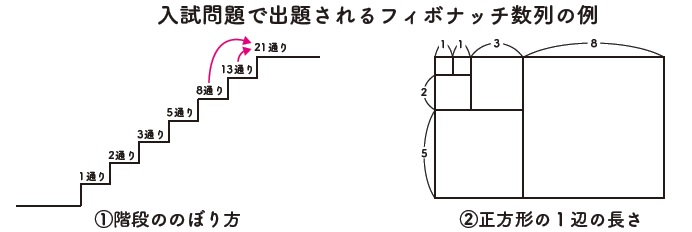
灘 開成の入試に頻出 図形に潜む フィボナッチ数列 の問題 富裕層向け資産防衛メディア 幻冬舎ゴールドオンライン

フィボナッチ数列 医療法人社団ヨシダ歯科 北海道 登別市

螺旋階段を上から覗いたときに見える形のフィボナッチ数列の螺旋の Yahoo 知恵袋

数学b フィボナッチ数列の絵本と階段 学習村の とりあえず国公立へ行こう

Withe通信 フィボナッチ数列と黄金比と美 Withe 広大生学習支援団体 Note

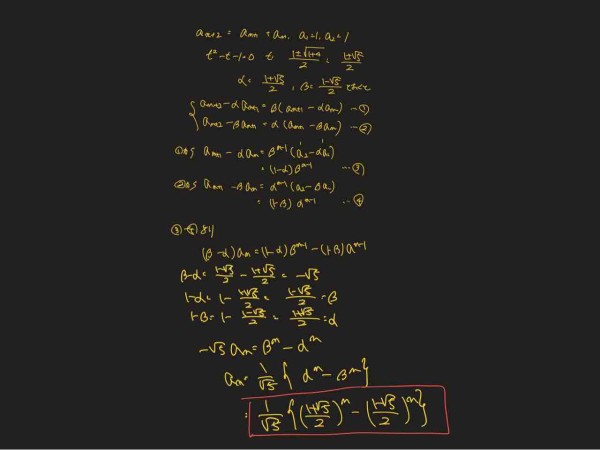
数学b フィボナッチ数列の絵本と階段 学習村の とりあえず国公立へ行こう

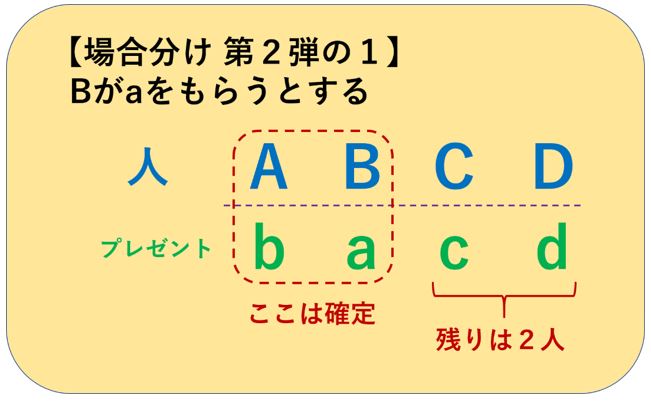
階段上りとフィボナッチ数列と場合分け 中学受験プロ講師ブログ

フィボナッチ数 Wikipedia

階段の昇り方の数列 21年浜松医科大学前期数学第3問 理系のための備忘録

フィボナッチ数列に感動 気まま日記 楽天ブログ

Toukou

数学小話 フィボナッチ数列 黄金数 の神秘 日比谷高校のススメ

算数テク フィボナッチ数列 タイル問題 中学受験算数なら開成卒プロ家庭教師k

階段の上り方 フィボナッチの数列 中学受験算数超特急シリーズ 無料版

陰陽からのフィボナッチ数列ベクトル的生命現象形成の力学 なんでも哲学する 無双 太極 Ps陰陽論nonpolar Taiji Platonic Synergy Yin Yang Theory 日本心的革命宣言

フィボナッチ数列とは 問題に隠れた規則性に気づけるようにしよう 中学受験ナビ

階段上りとフィボナッチ数列と場合分け 中学受験プロ講師ブログ

第１回 フィボナッチ数列 ガスコン研究所

フィボナッチ数列 京極一樹の数学塾

フィボナッチ数列をわかりやすく解説 一般項の求め方をマスターしよう Studyplus スタディプラス

001 フィボナッチ数列 コマ大数学科 Qiita

フィボナッチ数列とは 一般項から 黄金比 と呼ばれる理由まで解説 高校生向け受験応援メディア 受験のミカタ

フィボナッチ数列と黄金比 ブルズアイufo 楽天ブログ

フィボナッチ数列 数学入試問題

算数テク フィボナッチ数列 タイル問題 中学受験算数なら開成卒プロ家庭教師k

ガウディの足跡１０ サグラダファミリア 内部 Cafe Mare Nostrum

予習シリーズ 6年生上 第5回 理解を深めよう Youtube

フィボナッチ数列のスマホ壁紙 検索結果 1 画像数134枚 壁紙 Com

フィボナッチ数列とは 問題に隠れた規則性に気づけるようにしよう 中学受験ナビ

第３２問の解答

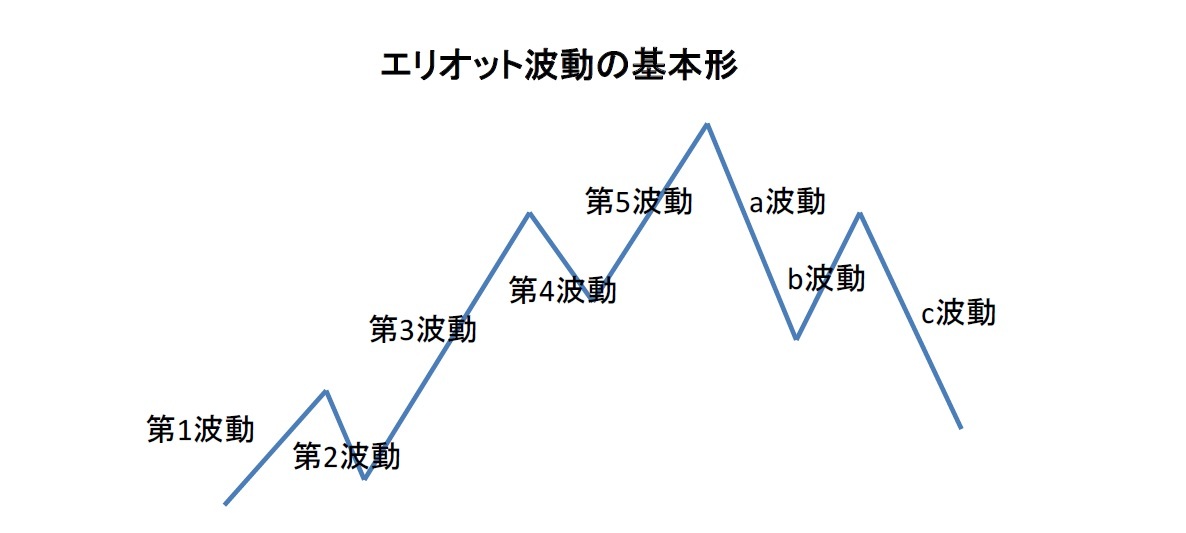
フィボナッチ数列について その３ フィボナッチ数列はどこで使用され どんな場面に現れてくるのか 自然界以外 ニッセイ基礎研究所

算数テク トリボナッチ数列 階段問題 中学受験算数なら開成卒プロ家庭教師k

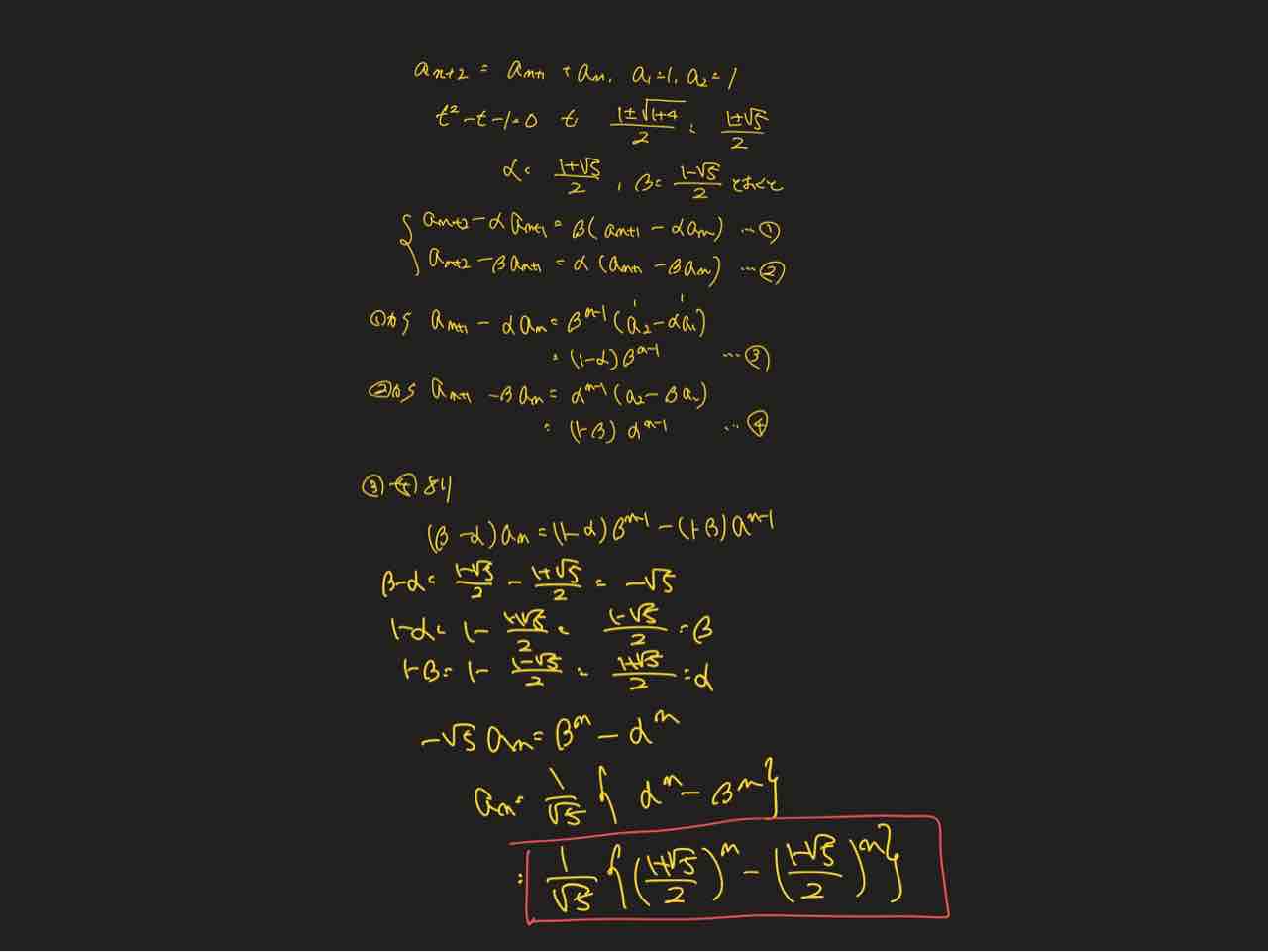
数学b フィボナッチ数列の絵本と階段 学習村の とりあえず国公立へ行こう

フィボナッチ数列と美の関係 ヘアスタイルにも当てはまる 小原昇隼 氏 Devonshire Hairstudio 金田健 氏 Sherpath代表 教育対談 Singalife 在シンガポール日本人向けのフリーマガジン グルメ 習い事 ビジネス 教育など充実の内容満載のウェブサイト

今月の問題

美術館 ももか Note

フィボナッチ数を極める

3分でわかる算数 階段の上り方は何通り フィボナッチ数列を知ろう 元四谷大塚sコース生による中学受験のツボ

11年 千葉大 8 数学入試問題

Incoming Term: フィボナッチ数列 階段, フィボナッチ数列 階段 漸化式, フィボナッチ数列 階段 一般項,